Modeling With NMF And SVD

---

Why we decomposing a matrix:

Decomposing matrices into matrices that have special properties.

Where we can use it?

• semantic analysis
• collaborative filtering/recommendations (winning entry for Netflix Prize)
• calculate Moore-Penrose pseudoinverse
• data compression
• principal component analysis

How we can decompose a matrix

• SVD
• NMF

SVD

Eg: image composition
SVD is an exact decomposition, since the matrices it creates are big enough to fully cover the original matrix(you can recover your matrix).

Singular value:

Can give us kind of measure of importance of matrix

Ranking

How to separate different topics?

We would clearly expect that the words that appear most frequently in one topic would appear less frequently in the other - otherwise that word wouldn’t make a good choice to separate out the two topics. Therefore, we expect the topics to be orthogonal(eg: columns of $U$ or rows of $V$ are orthogonal).

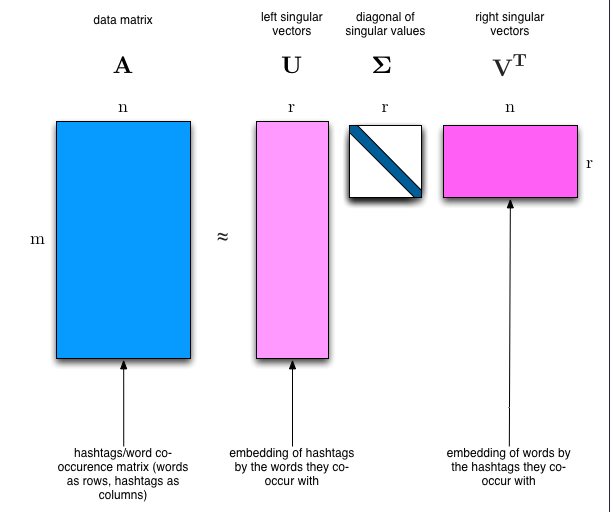
What the matrix means in a intuitive way?

$U$ row direction means the first column of matrix $A$, and columns means topics, they are orthogonal.
$S$ is diagonal matrix and ordered in descending order, give us a sense of importance.(topics by topics)
$V$ row direction means topics, and column direction means different words frequencies.

#how to show that the result of linalg.svd is a decomposition of the input
import numpy as np
from sklearn.datasets import fetch_20newsgroups
from sklearn import decomposition
from scipy import linalg
import matplotlib.pyplot as plt
categories = ['alt.atheism', 'talk.religion.misc', 'comp.graphics', 'sci.space']
remove = ('headers', 'footers', 'quotes')
newsgroups_train = fetch_20newsgroups(subset='train', categories=categories, remove=remove)
newsgroups_test = fetch_20newsgroups(subset='test', categories=categories, remove=remove)
num_topics, num_top_words = 6, 8
from sklearn.feature_extraction.text import CountVectorizer, TfidfVectorizer
vectorizer = CountVectorizer(stop_words='english')
vectors = vectorizer.fit_transform(newsgroups_train.data).todense() # (documents, vocab)
vectors.shape #, vectors.nnz / vectors.shape[0], row_means.shape
vocab = np.array(vectorizer.get_feature_names())
%time U, s, Vh = linalg.svd(vectors, full_matrices=False)
n = U @ np.diag(s) @ Vh
np.linalg.norm(n-vectors)  ## which is very small

## how to show that U and V are orthonormal
np.allclose (U @ U.T, np.eye(U.shape[0]))
np.allclose (Vh @ Vh.T, np.eye(U.shape[0]))

# show topics that are biggest
num_top_words=8

def show_topics(a):
    top_words = lambda t: [vocab[i] for i in np.argsort(t)[:-num_top_words-1:-1]]
    topic_words = ([top_words(t) for t in a])
    return [' '.join(t) for t in topic_words]
show_topics(Vh[:10])

NMF

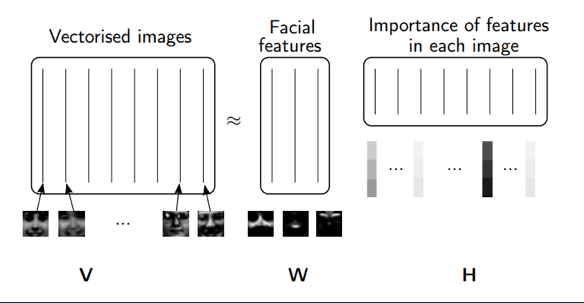
Rather than constraining our factors to be orthogonal, another idea would to constrain them to be non-negative. NMF is a factorization of a non-negative data set $V$: $V = W H$ into non-negative matrices $W,\; H$. Often positive factors will be more easily interpretable (and this is the reason behind NMF’s popularity).

Benefits: Fast and easy to use!
Downsides: Took years of research and expertise to create

Applications of NMF

• Face Decompositions
• Collaborative Filtering, eg movie recommendations
• Audio source separation
• Chemistry
• Bioinformatics and Gene Expression
• Topic Modeling (our problem!)

SGD

Applying SGD to NMF
Goal: Decompose $V\;(m \times n)$ into $V \approx WH$ where $W\;(m \times d)$ and $H\;(d \times n)$, $W,H > 0$, and we’ve minimized the Frobenius norm of $V-WH$.
Approach: We will pick random positive $W$ & $H$, and then use SGD to optimize.
To use SGD, we need to know the gradient of the loss function.

---

You May Also Enjoy

How To Train Multiple Model In One Time With Sklearn --Machine Learning

A Least Squares Approach --Machine Learning --Math

Linear Modeling - A Maximum Likelihood Approach --Machine Learning --Math

The Bayesian Approach To Machine Learning --Machine Learning --Math

An Introduction To ESN --Math

Feature Engineering For Machine Learning --Machine Learning

Welcome to share or comment on this post: